

This is an isosceles triangle in which two sides are equal, and also two angles are equal. Find the value of angle x in the triangle below. Worked examples on different types of triangles. Draw a line down from the vertex between the two equal sides, that hits the base at a right angle. The area of a triangle is equal to the product of the base and the height. Please make a donation to keep TheMathPage online. Divide the isosceles into two right triangles. We remember that all sides and all angles are equal in the. Let's start with the trigonometric triangle area formula: area (1/2) × a × b × sin (), where is the angle between the sides. and in each equation, decide which of those three angles is the value of x. Substituting h into the first area formula, we obtain the equation for the equilateral triangle area: area a × 3 / 4. Inspect the values of 30°, 60°, and 45° - that is, look at the two triangles. Therefore, the remaining sides will be multiplied by. In other words, each side must have a different length. The Scalene Triangle has no congruent sides. In the triangle ABC (given above), AB and AC are the two legs of the isosceles triangle. The Isosceles triangle shown on the left has two equal sides and two equal angles. The student should sketch the triangles and place the ratio numbers.Īgain, those triangles are similar. Legs: The two equal sides of an isosceles triangle are known as ‘legs’. An isosceles triangle is a triangle with two sides of equal length (and two angles of equal measure). Thus in an isosceles triangle to find altitude we have to draw a perpendicular from the vertex which is. It is unlike the equilateral triangle because there we can use any vertex to find out the altitude of the triangle. For any problem involving 45°, the student should sketch the triangle and place the ratio numbers. An isosceles triangle is a triangle with two sides of equal length and two equal internal angles adjacent to each equal sides. (For the definition of measuring angles by "degrees," see Topic 3.)Īnswer.
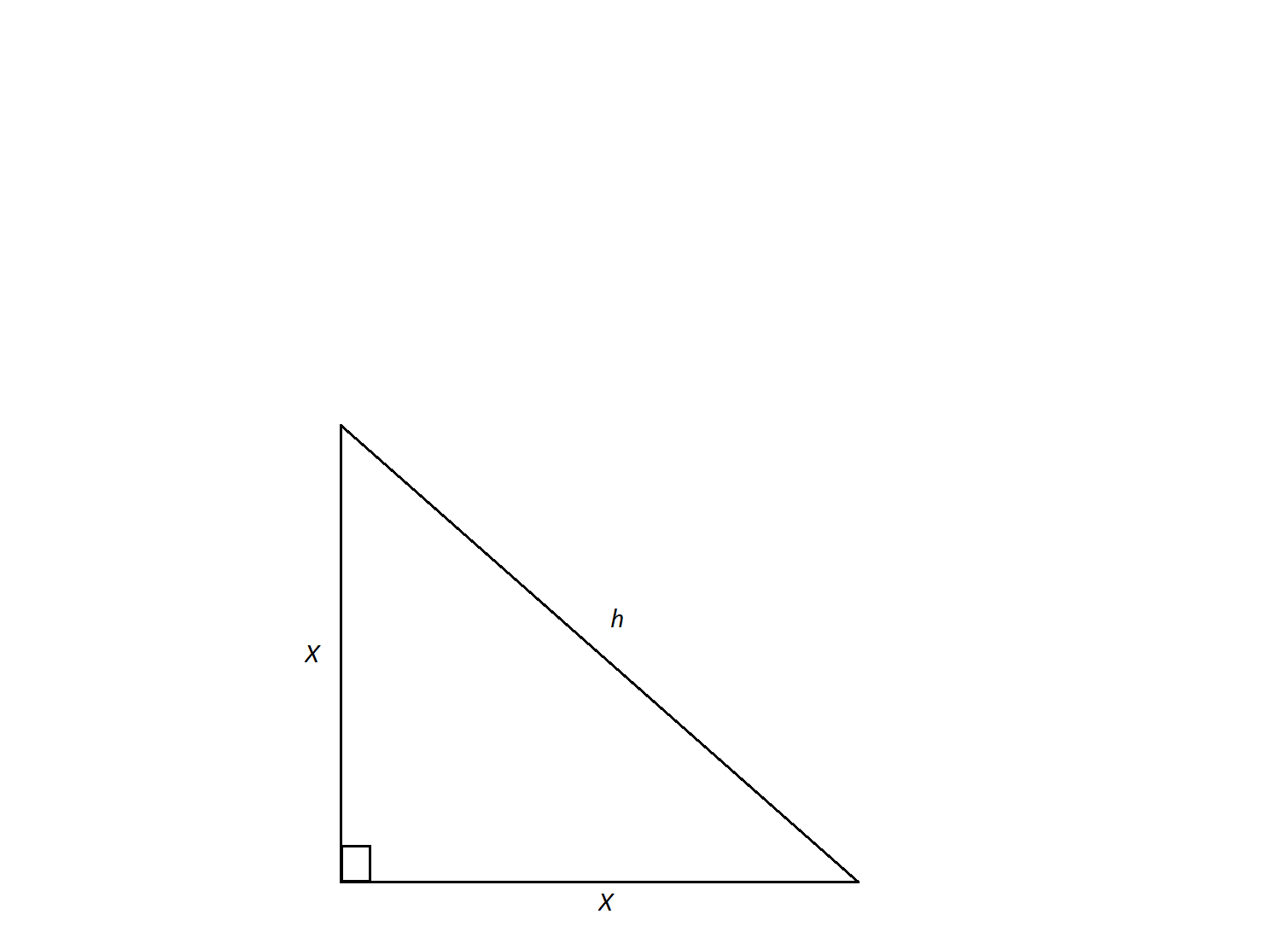
( Theorem 3.) Therefore each of those acute angles is 45°. Since the triangle is isosceles, the angles at the base are equal. ( Lesson 26 of Algebra.) Therefore the three sides are in the ratio An isosceles triangle has two sides of equal length and two equal sides join at the same angle to the base i.e. To find the ratio number of the hypotenuse h, we have, according to the Pythagorean theorem, In an isosceles right triangle, the equal sides make the right angle. In an isosceles right triangle the sides are in the ratio 1:1. The theorems cited below will be found there.) See Definition 8 in Some Theorems of Plane Geometry. (An isosceles triangle has two equal sides. (The other is the 30°-60°-90° triangle.) In each triangle the student should know the ratios of the sides. Topics in trigonometryĪ N ISOSCELES RIGHT TRIANGLE is one of two special triangles. It is the 2 sides which are opposite the 2 equal base angles which are equal in length.The isosceles right triangle. Make sure that you get the equal sides and angles in the correct position. To find the ratio number of the hypotenuse h, we. The common mistake is identifying the wrong sides as the equal (congruent sides). In an isosceles right triangle, the equal sides make the right angle. Seeing the triangles in different positions will help with this understanding.įor example, here is a picture where the base angles of an isosceles triangle are on the top. Here is a list of a few properties of isosceles triangles: An isosceles triangle has two equal sides and two equal angles. A triangle with all sides equal is called an equilateral triangle, and a triangle with no sides equal is called a scalene triangle.
#Isosceles triangle sides are equal iso#
The name derives from the Greek iso (same) and skelos (leg). The common mistake is thinking that the base of the angles are always on the bottom of the isosceles triangle. An isosceles triangle therefore has both two equal sides and two equal angles. So when students classify the triangles, they wind up classifying them incorrectly.
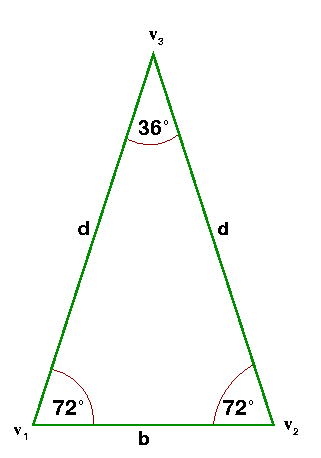
However, equilateral triangles have three equal (congruent) sides and angles and can be classified as isosceles.Ī common mistake when classifying triangles is mixing up the definitions of acute angle and obtuse angle. Isosceles triangles only have two equal (congruent) sides and angles and cannot be classified as equilateral. Understanding that properties of isosceles triangles and equilateral triangles can help with questions like this. The easy mistake to make is stating that isosceles triangles can be classified as equilateral triangles. Thinking that isosceles triangles can be classified as equilateral trianglesĪ question may ask students to explain if an isosceles triangle can be equilateral.


 0 kommentar(er)
0 kommentar(er)
